8+ this diagram is a straightedge and compass construction.
Using this it becomes relatively easy to answer such classical problems of geometry as. In other words the dimension is the number of independent parameters or coordinates that are needed for defining the position of a point that is constrained to be on the object.

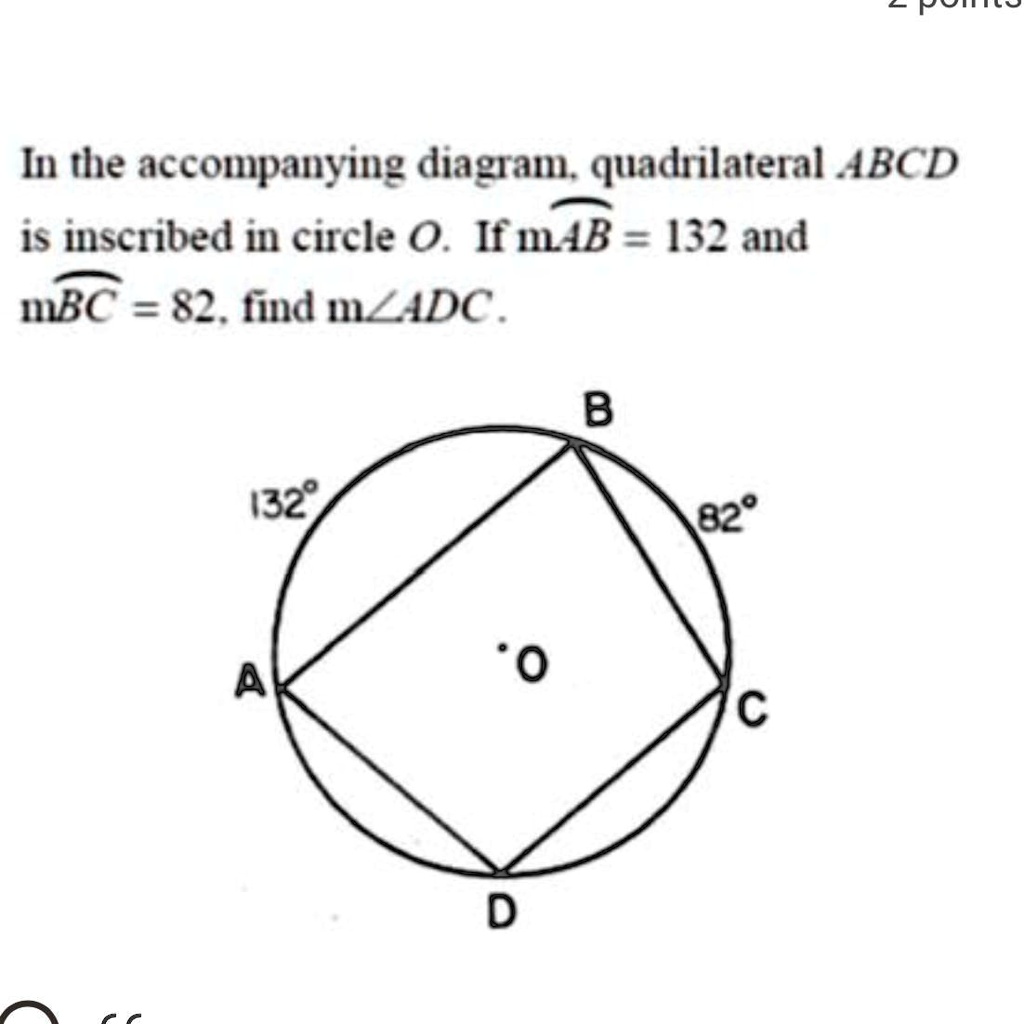
Illustrative Mathematics Geometry Mathematics Unit 1 Lesson 5 Formative Library Library Formative
The principal square root function usually just referred to as the square root function is a function that maps the set of nonnegative real numbers onto itself.
. There are 16 subgroups. ASCII characters only characters found on a standard US keyboard. Let E n be the statement that in a triangulation of a simple polygon with n sides at least one of the triangles in the triangulation has two sides bordering the exterior of the polygon.
The segment is bisected by drawing intersecting circles of equal radius whose centers are the endpoints of the segmentThe line determined by the points of intersection of the two circles is. Probe indicators typically consist of a graduated dial and needle driven by a clockwork thus the clock terminology to record the minor increments with a smaller embedded clock face and needle to record the number of needle rotations on the main dial. It gives an elegant characterization of the ratios of lengths that can be constructed with this method.
The linear eccentricity c is the distance between the center and a focus. In geometrical terms the square root function maps the area of a square to its side length. An unmarked straightedge and a compass.
Pierre Wantzel proved in 1837 that the problem as stated is impossible to solve for arbitrary angles. 287 BC in the seaport city of Syracuse Sicily at that time a self-governing colony in Magna GraeciaThe date of birth is based on a statement by the Byzantine Greek historian John Tzetzes that Archimedes lived for 75 years before his death in 212 BC. Squaring the circle is a problem in geometry first proposed in Greek mathematicsIt is the challenge of constructing a square with the area of a circle by using only a finite number of steps with a compass and straightedgeThe difficulty of the problem raised the question of whether specified axioms of Euclidean geometry concerning the existence of lines and circles implied.
In addition to the eccentricity e foci and directrix various geometric features and lengths are associated with a conic sectionThe principal axis is the line joining the foci of an ellipse or hyperbola and its midpoint is the curves centerA parabola has no center. AB BC CD DABut since in Euclidean. It is of great importance in mathematics not only in the measurement of the circle but also in more advanced mathematics in connection with such topics as continued fractions.
The square root of x is rational if and only if x is a rational number that can be represented as a ratio of two perfect squares. 195194 BC was a Greek polymath. 6 to 30 characters long.
A quick proof can be obtained by looking at the ratio of the areas of the two triangles and which are created by the angle bisector in Computing those areas twice using different formulas that is with base and altitude and with sides and their enclosed angle will yield the desired result. Based on this definition complex numbers can be added and. Place the fixed leg of the compass on the centre point the movable leg on the point on the circle and rotate the compass.
The latus rectum is the chord parallel to the. For example the dimension of a point is zero. The golden ratio was called the extreme and mean ratio by Euclid and the divine proportion by Luca Pacioli and also goes by several other names.
We use these notations for the sides. In a right triangle the square of the hypotenuse is equal to the sum of theDISCRETE MATH. The symbol for pi is π.
A plan diagram is the basic architectural diagram. A mathematician geographer poet astronomer and music theoristHe was a man of learning becoming the chief librarian at the Library of AlexandriaHis work is comparable to what is now known as the study of geography and he. The spring-loaded probe or plunger moves perpendicularly to the.
Also known as the floor plan this drawing shows a scaled version of the building as a vertical orthographic projection. Angle trisection is a classical problem of straightedge and compass construction of ancient Greek mathematicsIt concerns construction of an angle equal to one third of a given arbitrary angle using only two tools. A complex number is a number of the form a bi where a and b are real numbers and i is an indeterminate satisfying i 2 1For example 2 3i is a complex number.
Archimedes was born c. In mathematics the dimension of an object is roughly speaking the number of degrees of freedom of a point that moves on this object. 276 BC c.
There are 8 up to isomorphism. Galois theory also gives a clear insight into questions concerning problems in compass and straightedge construction. The dial has fine gradations for precise measurement.
In Euclidean geometry a regular polygon is a polygon that is direct equiangular all angles are equal in measure and equilateral all sides have the same length. It is the ratio of a regular pentagons diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron. The simplest and most basic is the construction given the centre of the circle and a point on the circle.
Must contain at least 4 different symbols. Died 415 AD was a neoplatonist philosopher astronomer and mathematician who lived in Alexandria Egypt then part of the Eastern Roman EmpireShe was a prominent thinker in Alexandria where she taught philosophy and astronomy. Definition and properties of a hexagon with interactive animation and construction with compass and straightedge.
Both members and non-members can engage with resources to support the implementation of the Notice and Wonder strategy on this webpage. In mathematics the simplest form of the parallelogram law also called the parallelogram identity belongs to elementary geometryIt states that the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals. If two sides of a right angle are 7 cm and 8 cm then its third side will be 9 cm.
Construction with given diameter. In the Sand-Reckoner Archimedes gives his fathers name as Phidias an astronomer about whom. The ratio is the same for all circles and is approximately 31416.
Mathematicians have studied the golden ratios properties since antiquity. Let denote the height of the triangles on base and be half of the angle in. In mathematics the Pythagorean theorem or Pythagoras theorem is a fundamental relation in Euclidean geometry among the three sides of a right triangleIt states that the area of the square whose side is the hypotenuse the side opposite the right angle is equal to the sum of the areas of the squares on the other two sidesThis theorem can be written as an equation relating the.
There are many compass-and-straightedge constructions resulting in circles. The Voronoi diagram of a regular triangular lattice is the honeycomb tessellation of hexagons. This diagram highlights essential features such as windows doors stairs walls and even furniture.
This way a complex number is defined as a polynomial with real coefficients in the single indeterminate i for which the relation i 2 1 0 is imposed. Pi pi in mathematics the ratio of the circumference of a circle to its diameter. Itself D 6 2 dihedral.
In classical geometry the bisection is a simple compass and straightedge construction whose possibility depends on the ability to draw circles of equal radii and different centers. Eratosthenes of Cyrene ɛr ə ˈ t ɒ s θ ə n iː z. Regular polygons may be either convex star or skewIn the limit a sequence of regular polygons with an increasing number of sides approximates a circle if the perimeter or area is fixed or a regular apeirogon.
A plan diagram can be a two-dimensional or three-dimensional drawing. When students become active doers of mathematics the greatest gains of their mathematical thinking can be realized. Although preceded by Pandrosion another Alexandrine female mathematician she is the first female.

The Diagram Is A Straightedge And Compass Construction C Is The Center Of Both Circles Which Of Brainly Com

The Diagram Is A Straightedge And Compass Construction A Is The Center Of One Circle And B Is The Brainly Com
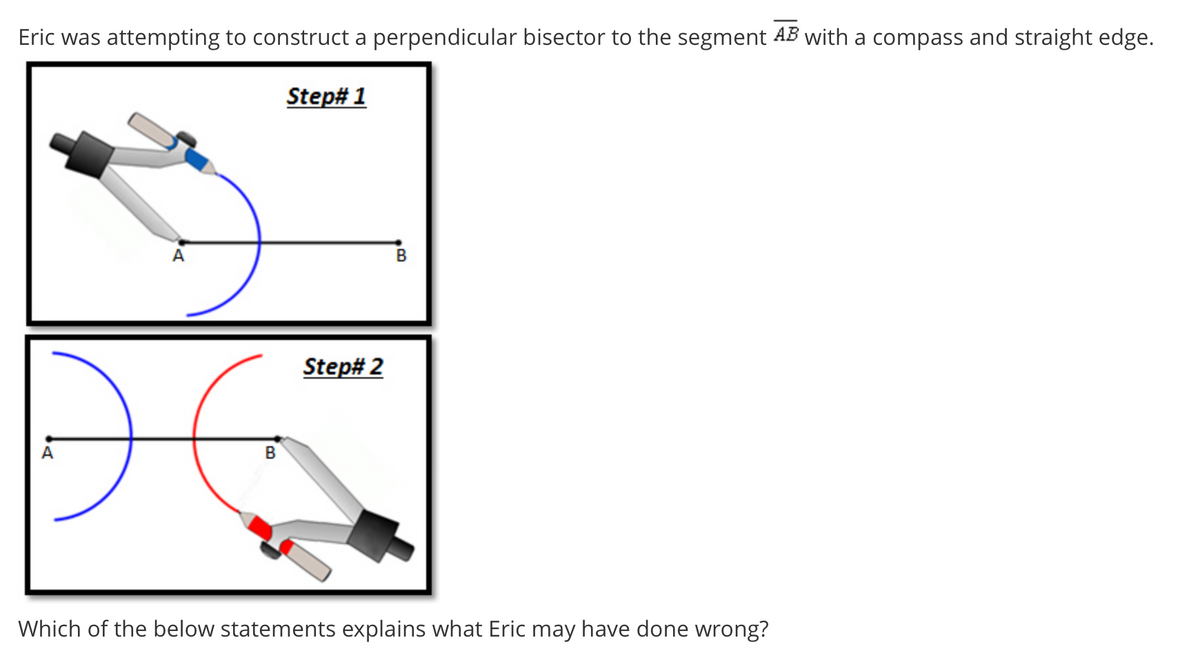
Answered Eric Was Attempting To Construct A Bartleby
6 This Diagram Is A Straightedge And Compass Cons Gauthmath

Answered Step 1 Draw A Line Segment On Your Bartleby
Construction

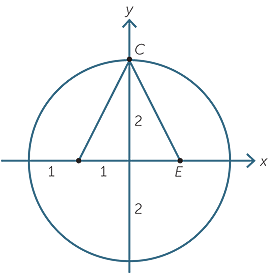
Illustrative Mathematics Geometry Mathematics Unit 1 Lesson 5 Formative Library Library Formative
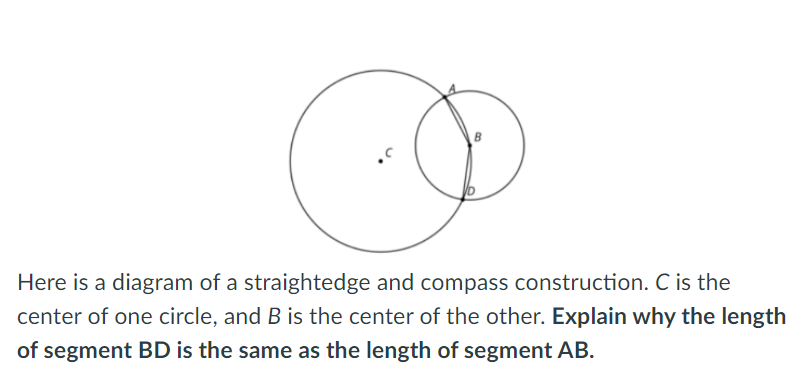
Answered Here Is A Diagram Of A Straightedge And Bartleby
What S The Easiest Way To Divide A Line Into 10 Equal Segments Without Using A Ruler Quora

The Diagram Is A Straightedge And Compass Construction A Is The Center Of One Circle And B Is The Brainly Com

Straightedge And Compass Construction Wikiwand

Constructions Quiz Quizizz
4 This Diagram Is A Straightedge And Compass Cons Gauthmath

Math Garden Compass And Straightedge Construction
Answered Use A Compass And Straightedge To Bartleby

Amazon Com Learning Resources Safe T Compass Orange Blister Card Classroom Safety Compass Geometric Tracer Ages 8 Geometry Compasses Office Products

Math Garden Compass And Straightedge Construction